8.1 SVM介绍以及从零开始公式推导
SVM介绍以及从零开始公式推导
还是老规矩,这一篇是对SVM进行介绍,下一篇博客就是使用SVM进行具体的使用。
SVM介绍
首先介绍SVM是什么,SVM(support vector machine)名为支持向量机,又名支持向量网络,是一个非常经典且高效的分类模型,是一种监督式的学习方法。
从名字上面来理解,SVM分为两个部分,"支持向量(support vector)"以及“机(machine)”。“machine”很简单的理解,就是算法的意思,那么“support vector”是什么呢? 这个现在不进行介绍,待我慢慢的引入。
线性分类
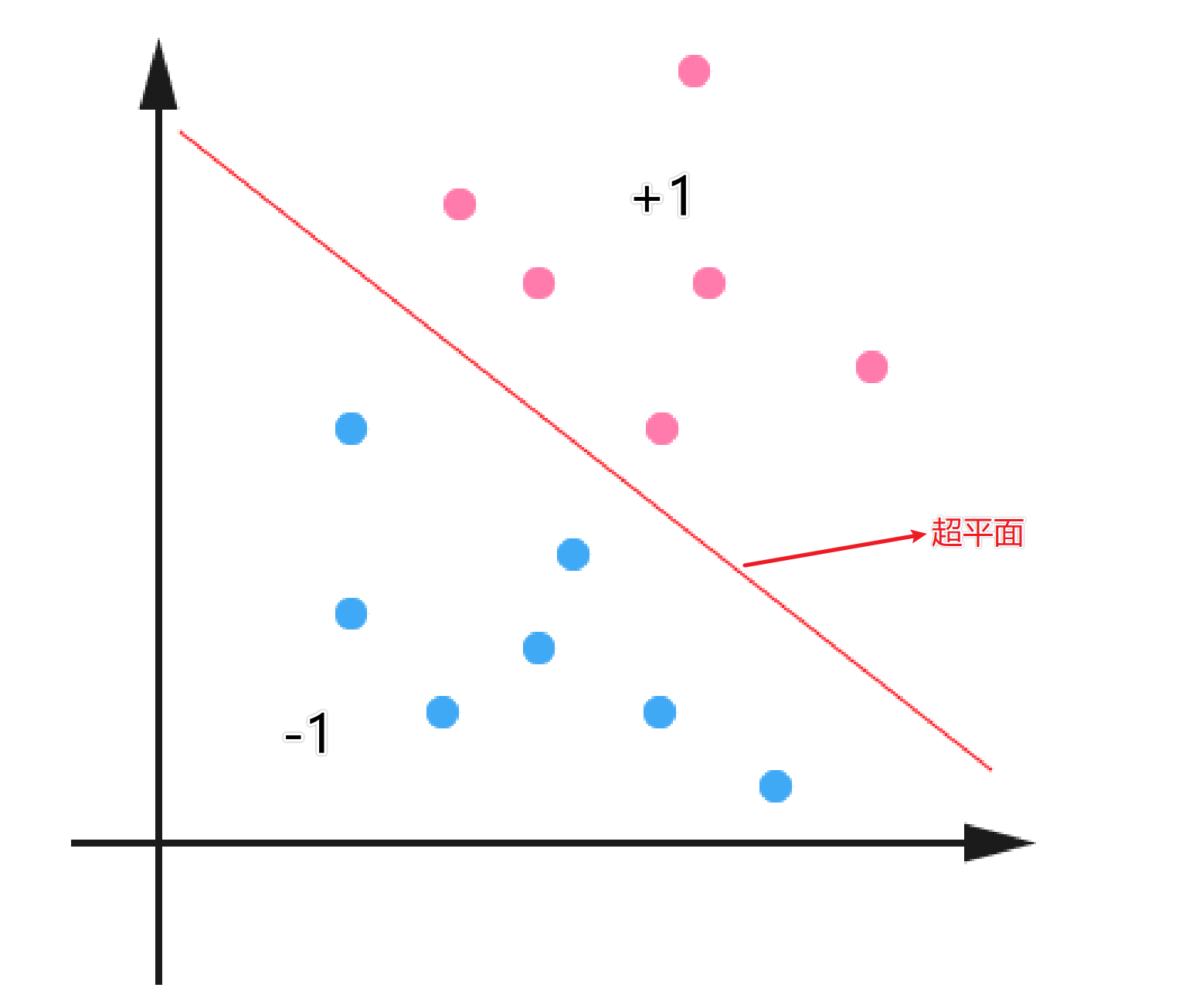
在介绍SVM之前,我们得先对线性分类器进行介绍。下面是一个二维平面的的分类问题,红色代表类别为$+1$,蓝色的代表类别是$-1$。中间的线就代表分割这两类问题的超平面。对于分类问题来说,红色和蓝色的点都是数据集中已知的,而我们的目的就是找到一个最适合的超平面,将数据进行分类。
对于线性二分类模型,给定一组数据$\left\{\left(\boldsymbol{x}_{1}, y_{1}\right),\left(\boldsymbol{x}_{2}, y_{2}\right), \ldots,\left(\boldsymbol{x}_{m}, y_{m}\right)\right\}$,其中$\boldsymbol{x}_{i} \in \mathbb{R}^{d}, y \in\{-1,1\}$,二分类任务的目标是希望从数据中学得一个假设函数$h: \mathbb{R} \rightarrow\{-1,1\}$,使得$h(x_i) = y_i$
$h\left(\boldsymbol{x}_{i}\right)=\left\{\begin{aligned}&1若y_{i}=1\\&-1若y_{i}=-1\end{aligned}\right.$
那么问题来了,我们如何去寻找一个能够将$y_i = \pm1$划分开的超平面?首先我们可以设超平面的函数是:
$f(\boldsymbol{x})=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b$
这里有一个值得注意的点,下面的这个公式会在后面的推导中经常用到。
$y_i^2 = 1$
尽管有很多的问题都是线性不可分的,但是呢,目前我们只讨论线性可分问题,到后面我们再讨论如何将非线性问题转成线性问题。因此,暂时我们不需要去纠结如果是非线性问题怎么办。
我们可以直观的从图中进行感受,这样的超平面是有多个的,那么如何寻找一个最合适的超平面呢(也就是寻找最合适的wT 和b)?接下来引出间隔的概念来寻找最合适的超平面。
间隔
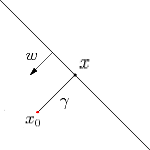
如下图所示,超平面$f(\boldsymbol{x})=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b$,则$x$为$x_0$到超平面的投影,$x_0$对应的类别是$y_0$,$w$为超平面的法向量,$γ$为$x_0$到超平面的距离(带正负号)。
因此,
$\gamma = \frac{f(x_0)}{||w||} \\ 因此距离(不带正负号)的为: \\ \tilde{\gamma} = y_0\gamma$
这样我们就推出了间隔的表达式$\tilde{\gamma} = y_0\gamma$。对于给定的数据集,我们当然是希望数据集中的数据离超平面越远越好,因为这样所能够容忍的误差也就越大。那么这个远如何来确定呢?接下来让我们讨论什么是最大间隔分类器。
最大间隔分类器
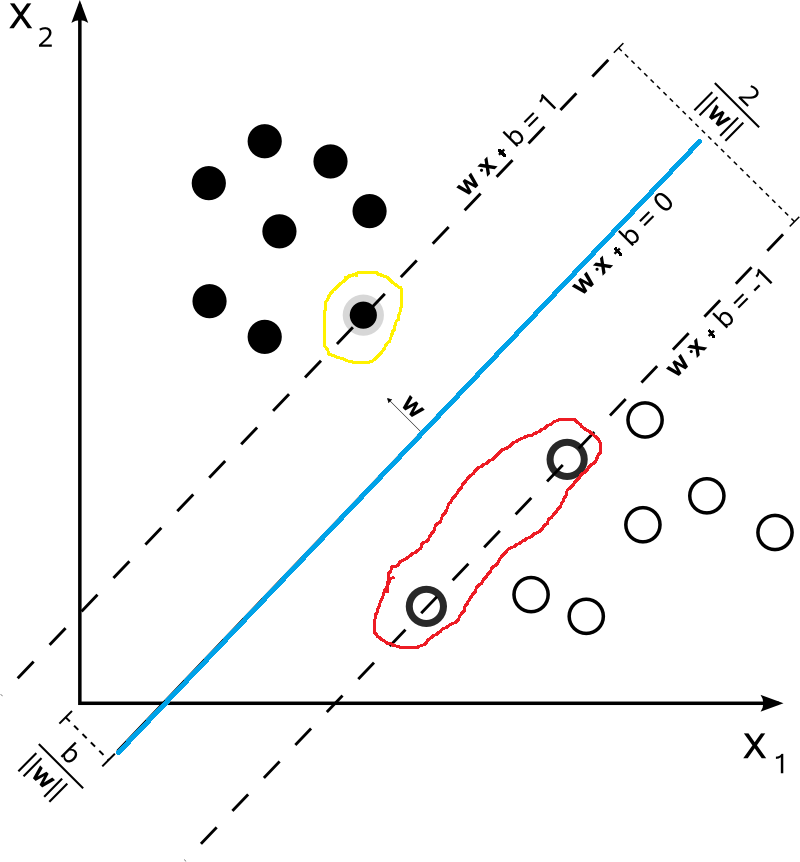
如果我们给定如下的数据集,那么对于下面的数据集,哪一些最不可能分类成功呢?毋庸置疑的,就是最靠近$f(\boldsymbol{x})=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b$超平面的数据点(比如下图中被红色和黄色圈出来的点)。而被圈出来的点也就是被称之为“支持向量”。因为在模型中我们考虑他们就可以了。
首先我们假设支持向量分布在$\omega^Tx+b=\pm 1$超平面上,这里取值为1只是为了方便,该值并不影响后面的优化结果。很显然,支持向量到超平面$\omega^Tx+b=\pm 1$的距离为$\frac{1}{\|\omega\|}$两侧的距离加起来就是$\frac{2}{\|\omega\|}$在前面我们说过,我们希望距离越大越好,也就是说$\frac{2}{\|\omega\|}$大越好,同时对于数据集中数据的分布满足$y(\omega^T+b)x \geqslant 1$。因此,我们得到了如下的优化问题
$ \left\{ \begin{aligned} \max \quad \frac{2}{\Vert \omega \Vert} \\ s.t. \quad y_i(\omega^T x_i + b) \geqslant 1 ,\quad i=1,2,...,m \end{aligned} \right.$
为了方便后续的推导,该优化问题等价于:
$ \left\{ \begin{aligned} \min \quad \frac{1}{2}\| \omega \|^2 \\ s.t. \quad y_i(\omega^T x_i + b) \geqslant 1 ,\quad i=1,2,...,m \geqslant 1 ,\quad i=1,2,...,m \end{aligned} \right.$
拉格朗日乘子法(Lagrange multipliers)
拉格朗日乘子法是一种寻找多元函数在一组约束下的极值的方法。通过引拉格朗日乘子,可将有$d$个变量与$k$个约束条件的最优化问题转化为具有$d+k$个变量的无约束优化问题求解。下面让我们来进行推导。
拉格朗日乘子法推导
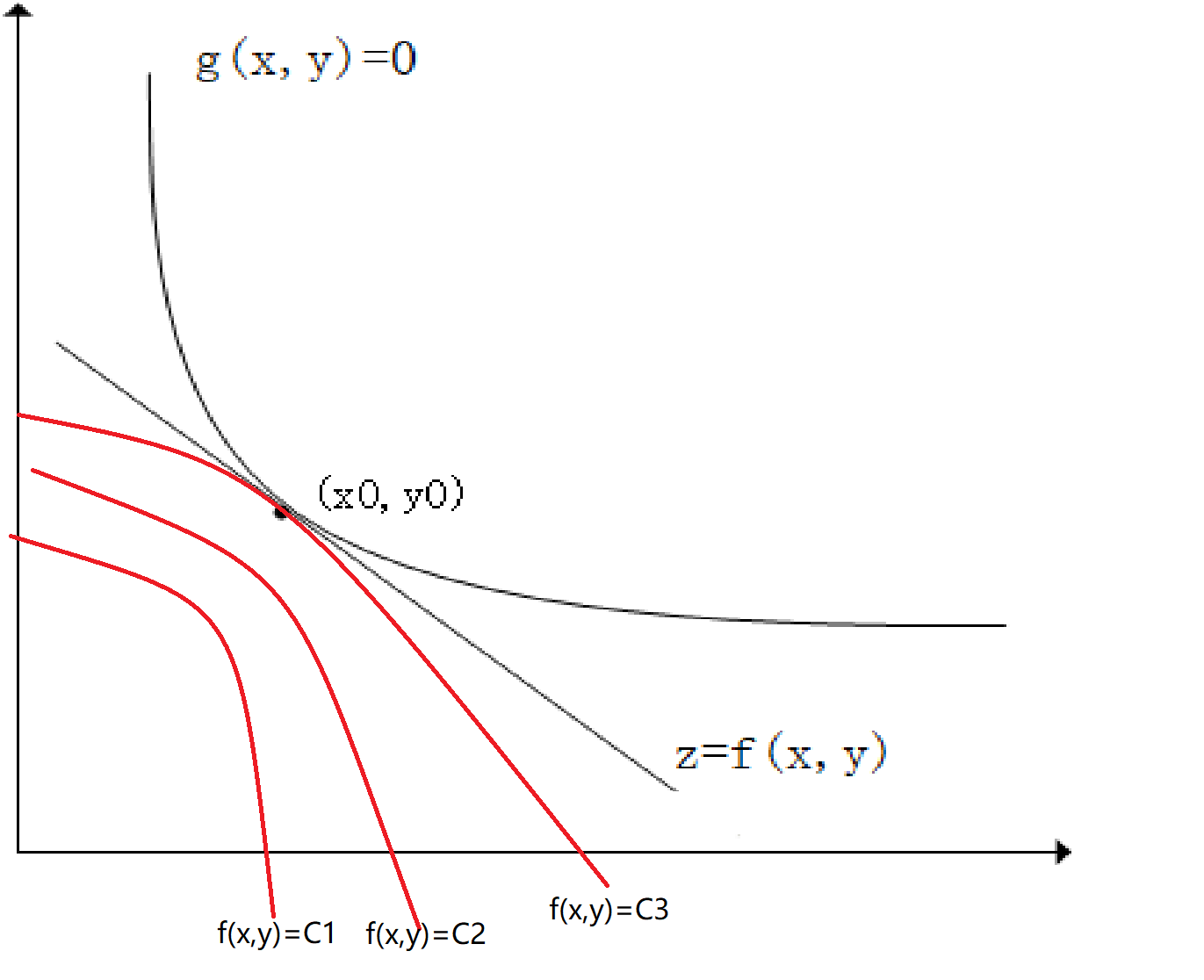
如下图所示$z=f(x,y)$,$g(x,y)=0$,如果我们需要求z在$g(x,y)$条件下的极值。从几何角度来说,我们可以画出$z = C_i$的等高线,等高线与$g(x,y)$相切的点$(x_0,y_0)$即为极值点。如下图所示:
因为在点$(x_0,y_0)$取得极值,那么,$\nabla{f(x_0, y_0)} // \nabla{g(x_0, y_0)}$也就是说此时梯度平行。也就是说$({f_x}'(x_0,y_0),{f_y}'(x_0,y_0)) // ({g_x}'(x_0,y_0),{g_y}'(x_0,y_0))$(这个是可以证明的,但是在这里就不证明了)因此有:
$\frac{{f_x}'(x_0,y_0)}{{g_x}'(x_0,y_0)}=\frac{{f_y}'(x_0,y_0)}{{g_y}'(x_0,y_0)}=-\lambda_0 (\lambda_0可以为0)$
即:
$ \left\{\begin{aligned} {f_x}'(x_0,y_0)+\lambda_0{g_x}'(x_0,y_0)=0\\ \\ {f_y}'(x_0,y_0)+\lambda_0{g_y}'(x_0,y_0)=0\\ \\ g(x,y)=0 \end{aligned} \right.$
如果此时我们有一个辅助函数$L(x,y, \lambda)=f(x,y)+\lambda g(x,y)$,对其求偏导然后求极值点可得:
$ \left\{\begin{aligned} \frac{\partial L(x,y, \lambda)}{\partial x}={f_x}'(x,y)+\lambda{g_x}'(x,y)=0\\ \\ \frac{\partial L(x,y, \lambda)}{\partial y}={f_y}'(x,y)+\lambda{g_y}'(x,y)=0\\ \\ \frac{\partial L(x,y, \lambda)}{\partial \lambda}=g(x,y)=0 \end{aligned} \right.$
显而易见以上两个公式相等。因此我们对$z = f(x,y)$<在条件$f(x,y) = 0$的条件下求极值$(x_0,y_0)$的问题变成了求拉格朗日函数$L(x,y, \lambda)=f(x,y)+\lambda g(x,y)$偏导数为0的解。
KKT条件(Karush-Kuhn-Tucker Conditions)
上面我们讨论的是在等式约束条件下求函数极值的问题(也就是$g(x,y)=0$)but,如果如果是不等式条件下,我们应该如何来使用拉格朗日函数来求解呢?下面引出KKT条件。
什么是KKT条件呢?它是在满足一些有规则的条件下,一个非线性规划问题能有最优化解法的一个必要条件。也就是说优化问题在最优值处必须满足KKT条件。
例如我们有以下优化问题:
$\begin{aligned} \min _{x} & f(x) \\ \text { s.t. } & h_{i}(x)=0 \quad(i=1, \ldots, m) \\ & g_{j}(x) \leqslant 0 \quad(j=1, \ldots, n) \end{aligned}$
其拉格朗日函数为:
$L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu})=f(\boldsymbol{x})+\sum_{i=1}^{m} \lambda_{i} h_{i}(\boldsymbol{x})+\sum_{j=1}^{n} \mu_{j} g_{j}(\boldsymbol{x})$
则其KKT条件为:
$\left\{\begin{array}{l} g_{j}(\boldsymbol{x}) \leqslant 0 \\ \mu_{j} \geqslant 0 \\ \mu_{j} g_{j}(\boldsymbol{x})=0 \\ h(x) =0 \end{array}\right.$
接下来让我们来解释一下为什么是这样的。(不一定是数学证明)。
下面我们只讨论$f(x)$在不等式$gi(x)<0$条件下取$min$情况。这里可能有人会说,如果我要求$max$怎么办?很简单那,将$f(x)$取反即可,就变成了求min的情况。同样对于$gi(x)>0的情况,我们取反就变成了$g^{'}(x) = -g_i(x) \lt 0$。
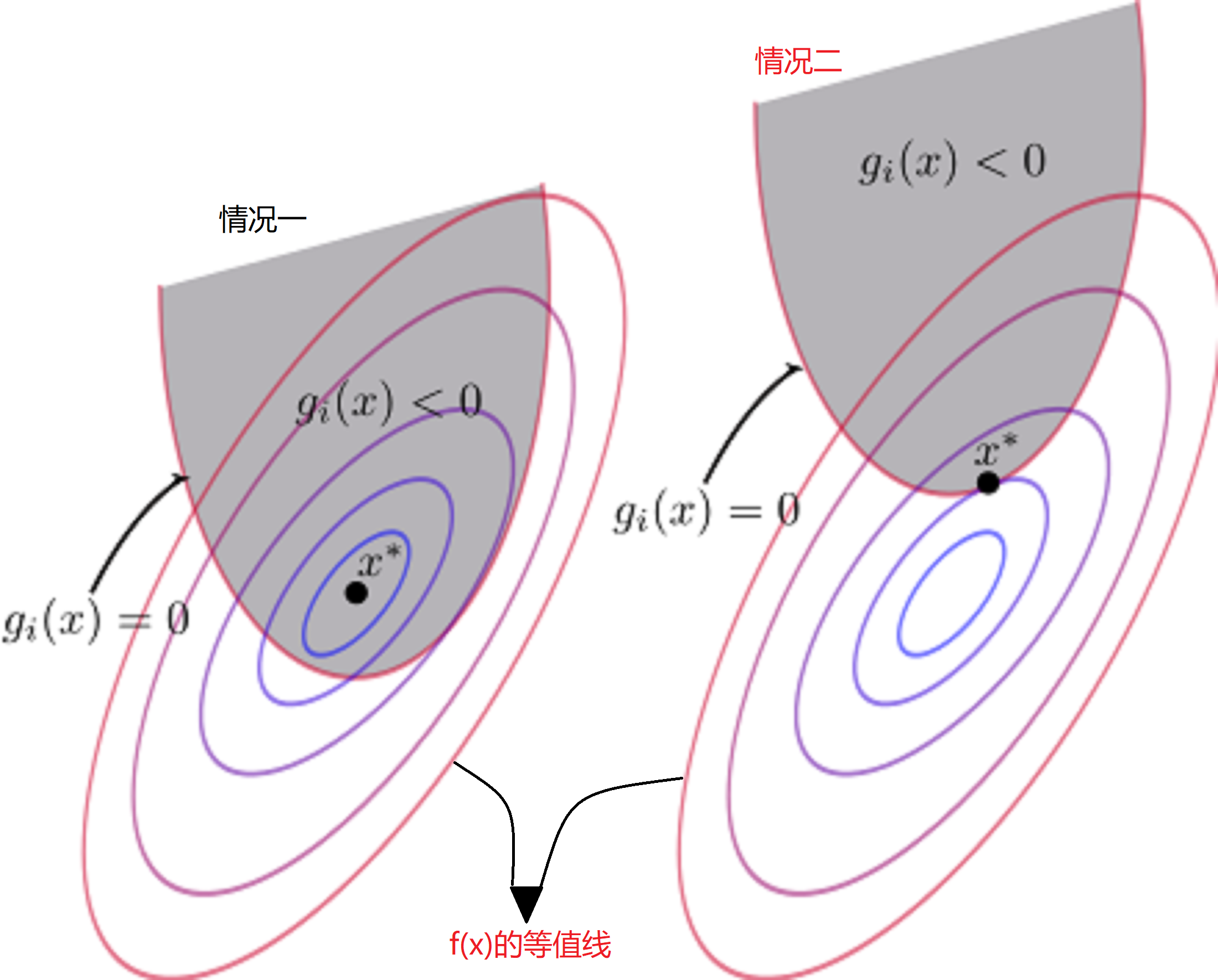
对于上述讨论,有两种情况如下图(图中$x^*$代表极小值点):
- 情况一:极小值点$x^*$在$g_i(x)<0的区域内
- 情况二:极小值点$x^*$在$g_i(x)=0$上
首先我们先讨论情况二,对于情况二很好理解,此时的“不等式约束”变成了“等式约束”。那么其在极值点满足以下条件:
$h(x)=0\\ g(x)=0\\ \mu \geq 0$
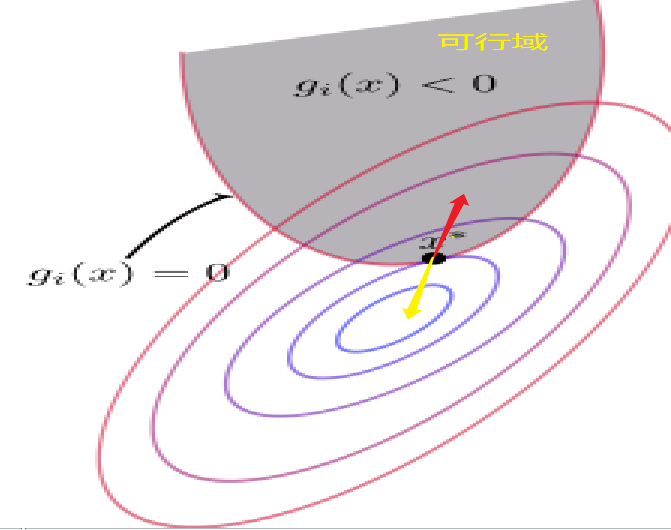
$h(x)=0,g(x)=0$我们很好理解,但是为什么我们对μ还要进行限制呢?然后为什么限制还为$\mu \geq 0$呢?首先我们来考虑一下$f(x)$和$g(x)$在$x^*$点的梯度方向(首先$f(x)$和$g(x)$在$x^*$点的梯度方向肯定是平行的【梯度的方向代表函数值增加最快的方向】)。
- 对于$f(x)$来说,等值线大小由中心到周围逐渐增大,因此它的梯度方向指向可行域。为图中红色的箭头号。
- 对于g(x)来说,梯度方向肯定是指向大于0的一侧,那么就是要背离可行域。为图中黄色的箭头号。
在前面拉格朗日乘子法中我们有以下推导:
$\frac{{f_x}'(x_0,y_0)}{{g_x}'(x_0,y_0)}=\frac{{f_y}'(x_0,y_0)}{{g_y}'(x_0,y_0)}=-\lambda_0 (\lambda_0可以为0)$
又因为$g(x)$和$f(x)$梯度方向相反,因此$\lambda_0 \geq0$。 因此对于公式9有μ≥0。
接下来让我们来讨论情况一。情况一是极小值$x^*$在$g(x)$的可行域中,因此,我们可以将其看成没有不等式约束条件。那么其在极值点满足以下条件:
$h(x)=0\\ g(x) \leq 0\\ \mu =0$
对比两种情况:
- 情况一:$\mu = 0,g(x) \leq 0$
- 情况二:$μ≥0,g(x)=0$
综合情况一和情况二,可得到KKT条件为:
$\left\{\begin{array}{l} g_{j}(\boldsymbol{x}) \leqslant 0 \quad(主问题可行)\\ \mu_{j} \geqslant 0 \quad(对偶问题可行)\\ \mu_{j} g_{j}(\boldsymbol{x})=0 \quad(互补松弛)\\ h(x) =0 \end{array}\right.$
拉格朗日乘子法对偶问题
对于如下优化问题:
$\begin{aligned} \min _{x} & f(x) \\ \text { s.t. } & h_{i}(x)=0 \quad(i=1, \ldots, m) \\ & g_{j}(x) \leqslant 0 \quad(j=1, \ldots, n) \end{aligned}$
其拉格朗日函数为:
$L(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu})=f(\boldsymbol{x})+\sum_{i=1}^{m} \lambda_{i} h_{i}(\boldsymbol{x})+\sum_{j=1}^{n} \mu_{j} g_{j}(\boldsymbol{x}) \\ s.t. \mu_j \ge0$
对于上述的优化问题(公式10)我们可以等价于(下面的称之为主问题):
$\begin{aligned} \min _{x} \max _{\boldsymbol{\lambda}, \boldsymbol{\mu}} & \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \\ \text { s.t. } & \mu_{i} \geq 0, \quad i=1,2, \ldots, m \end{aligned}$
证明如下:
\begin{aligned} \min _{x} \max _{\boldsymbol{\lambda}, \boldsymbol{\mu}}\mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \\ =\min _{\boldsymbol{x}}\left(f(\boldsymbol{x})+\max _{\boldsymbol{\lambda}, \boldsymbol{\mu}}\left(\sum_{i=1}^{m} \mu_{i} g_{i}(\boldsymbol{u})+\sum_{j=1}^{n} \lambda_{j} h_{j}(\boldsymbol{u})\right)\right) \\ =\min _{\boldsymbol{x}}\left(f(\boldsymbol{x})+\left\{\begin{array}{l} 0 \text{ 若x满足约束}\\ \infty \text{否则} \end{array}\right)\right.\\ =\min _{\boldsymbol{u}} f(\boldsymbol{u}) \end{aligned}$
其中, 当$gi(x)$不满足约束时, 即$gi(x)>0$, 我们可以令$\mu=\infty$, 使得$\mu_ig_i(x) = \infty$; 当$h_j(x)$不满足约束时, 即$h_j(x)\ne0$, 我们可以取$\lambda_j = \infty$, 使得$\lambda_jh_j(x) = \infty$。当$x$满足约束时, 由于$\mu_i\ge0$,$g_i(x)\le0$, 则$\mu_ig_j(x)\le0$,因此我们可以取最大值0。 实际上也就是说如果公式10存在最优解,则最优解必须满足KKT条件。
对于公式10其对偶问题为:
$\begin{aligned} \max _{\boldsymbol{\lambda}, \boldsymbol{\mu}} \min _{x}& \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \\ \text { s.t. } & \mu_{i} \geq 0, \quad i=1,2, \ldots, m \end{aligned}$
对偶问题是主问题的下界(他们两个具有弱对偶性):
$p^* = \min _{x} \max _{\boldsymbol{\lambda}, \boldsymbol{\mu}} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) \ge \max _{\boldsymbol{\lambda}, \boldsymbol{\mu}} \min _{x} \mathcal{L}(\boldsymbol{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) = g^*$
你可以记忆成“廋死的骆驼比马大”,还看到一个记忆方法为“宁为凤尾不为鸡头”。hhh
证明如下:
$\max _{x} \min _{y} f(x, y) \leq \min _{y} \max _{x} f(x, y)\\ \text{let } g(x)=\min _{y} f(x, y)\\ \text{then }g(x) \leq f(x, y), \forall y\\ \therefore \max _{x} g(x) \leq \max _{x} f(x, y), \forall y\\ \therefore \max _{x} g(x) \leq \min _{y} \max _{x} f(x, y)$
构建神经网络
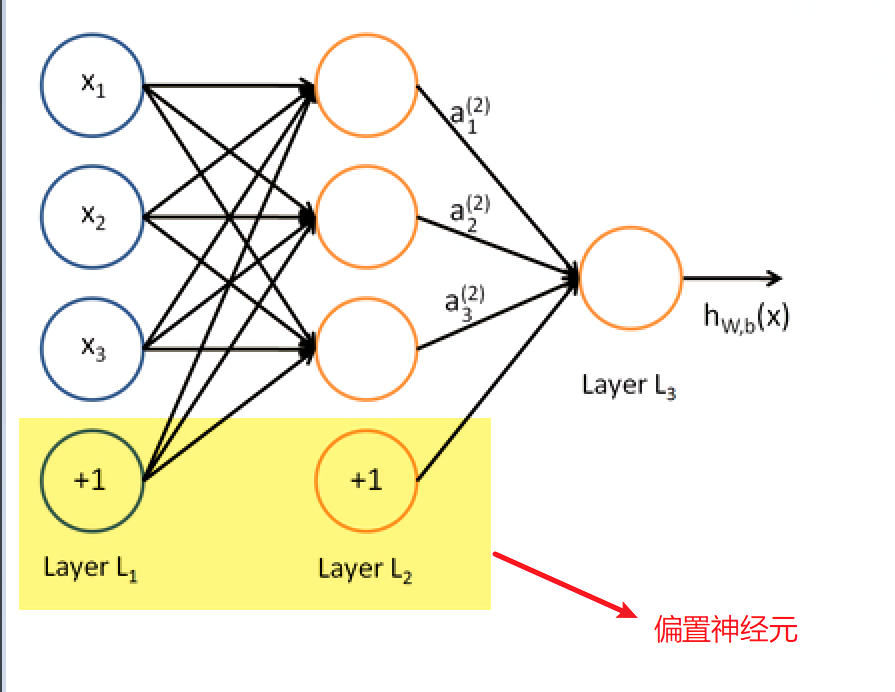
首先我们来创建一个神经网络,网络中只含有输入层,输出层和一层隐层。
from pybrain.tools.shortcuts import buildNetwork # X.shape[1]代表属性的个数,100代表隐层中神经元的个数,y.shape[1]代表输出 net = buildNetwork(X.shape[1],100, y.shape[1], bias=True)
这里说有以下“bias”的作用。bias代表的是偏置神经元,bias=True代表偏置神经元激活,也就是在每一层都使用这个这个神经元。偏置神经元如下图,实际上也就是阈值,只不过换一种说法而已。
现在我们已经构建好了一个比较简单的神经网络,接下来我们就是使用BP算法去得到合适的权重值了。
反向传播(BP)算法
具体的算法步骤在上一篇已经介绍过了,很幸运的是在pybrain中间提供了BP算法的库供我们使用。这里就直接上代码吧。关于BackpropTrainer更加细节的使用可以看官网
from pybrain.supervised.trainers import BackpropTrainer trainer = BackpropTrainer(net, train_data, learningrate=0.01,weightdecay=0.01)
这里面有几个参数稍微的说明下:
- net:神经网络
- train_data:训练的数据集
- learningrate:学习率,也就是下面的
$η$,同样它可以使用lrdecay这个参数去控制衰减率,具体的就去看官网文档吧。
$\Delta w_{h j}=\eta g_{j} b_{h} \\ \Delta \theta_{j}=-\eta g_{j} \\ \Delta v_{i h}=\eta e_{h} x_{i} \\ \Delta \gamma_{h}=-\eta e_{h} \\$
- weightdecay:权重衰减,权重衰减也就是下面的
λ
$E=\lambda \frac{1}{m} \sum_{k=1}^{m} E_{k}+(1-\lambda) \sum_{i} w_{i}^{2} \\ \lambda \in(0,1)$
然后我们就可以开始训练了。
$trainer.trainEpochs(epochs=100)$
$epochs$也就是训练集被训练遍历的次数。
接下载便是等待的时间了。等待训练集训练成完成。训练的时间跟训练集的大小,隐层神经元的个数,电脑的性能,步数等等有关。
切记切记,这一次的程序就不要在阿里云的学生机上面跑了,还是用自己的机器跑吧。尽管联想小新pro13 i5版本性能还可以,但是还是跑了一个世纪这么久,哎(耽误了我打游戏的时间)。
进行预测
通过前面的步骤以及等待一段时间后,我们就完成了模型的训练。然后我们就可以使用测试集进行预测。
predictions = trainer.testOnClassData(dataset=test_data)
$predictions$的部分数据,代表着测试集预测的结果:
然后我们就可以开始验证准确度了,这里继续使用F1评估。这个已经在前面介绍过了,就不再介绍了。
F1验证
这里有个地方需要注意,因为之前的$y_test$数据我们使用$one-hot encoding$进行了编码,因此我们需要先将$one-hot$编码转成正常的形式。
# 取每一行最大值的索引。 y_test_arry = y_test.argmax(axis =1)
然后使用F1值进行验证。
from sklearn.metrics import f1_score print("F-score: {0:.2f}".format(f1_score(predictions,y_test_arry,average='micro')))
然后结果如下:
F-Score:0.86
结果只能说还行吧,不是特别的差,但是也不是特别的好。
总结
项目地址:Github。尽管上面的准确度不咋地,只有$86%$,但是也还行吧,毕竟也是使用了一层隐层,然后隐层也只有100个神经元。
如果电脑的性能不够的话,可是适当的减少步数和训练集的大小,以及隐层神经元的个数。